수학은 풀이과정까지 꼼꼼하게,
체리팟만 가능합니다.
체리팟만 가능합니다.
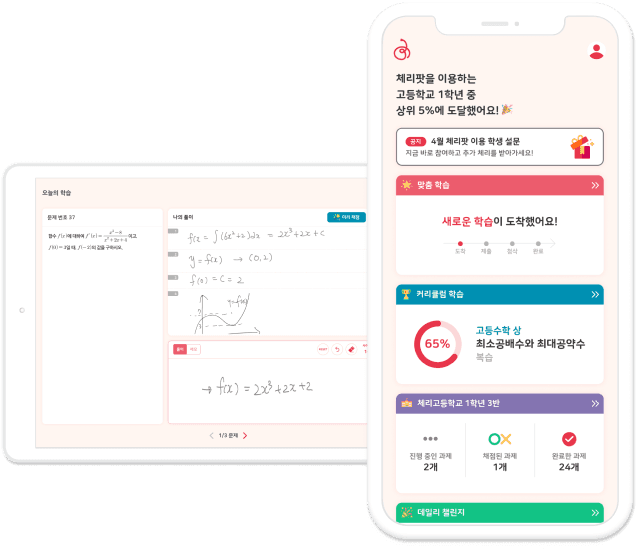
풀이과정 첨삭으로
가장 정확한 진단과 피드백
가장 정확한 진단과 피드백
수학은 맞았는지 틀렸는지가 아니라,
어디까지 알고 무엇을 모르는지가 중요합니다.
어디까지 알고 무엇을 모르는지가 중요합니다.
체리팟의 과정 중심 AI 기술은
손으로 작성한 풀이과정을 인식, 진단 후,
가장 정확한 피드백과 맞춤 학습을 제공합니다.
손으로 작성한 풀이과정을 인식, 진단 후,
가장 정확한 피드백과 맞춤 학습을 제공합니다.
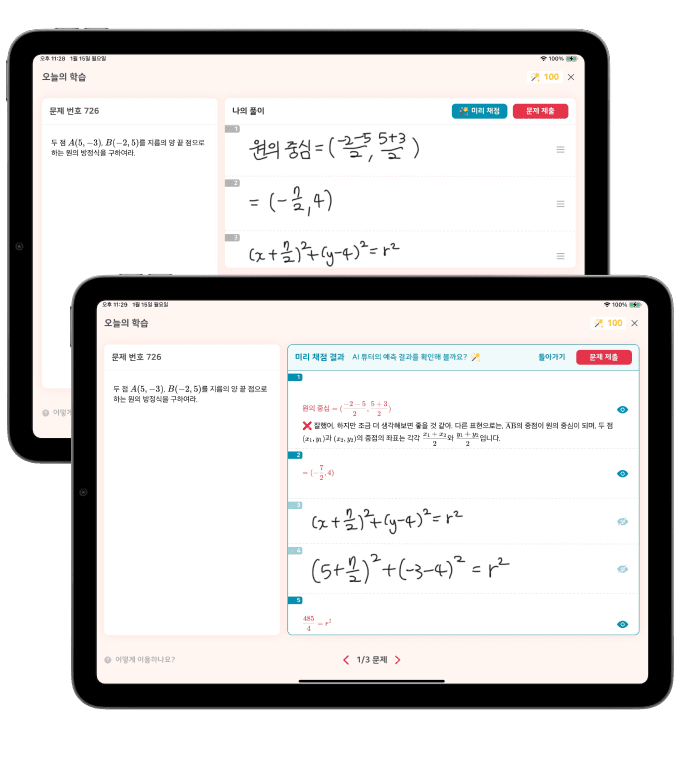
체리팟,
어떤 학교에서 사용하면 좋을까요?
어떤 학교에서 사용하면 좋을까요?

한 명씩 관리하기 힘든 저성취 학생!
효과적으로 괸리해주고 싶어요
효과적으로 괸리해주고 싶어요

과제 출제부터 오답 유형 분석까지,
AI로 스마트하게 하고 싶어요
AI로 스마트하게 하고 싶어요

수업을 잘 따라오고 있을까?
반별/학생별로 확인하고 싶어요
반별/학생별로 확인하고 싶어요
이제 체리팟과 함께
효율적인 맞춤 학습과 과제 관리를 시작해보세요!
효율적인 맞춤 학습과 과제 관리를 시작해보세요!
매일 나만을 위한
최적의 3문제를 찾아드려요
최적의 3문제를 찾아드려요
[체리팟 AI 맞춤학습 프로그램]
하루 3문제로 실력 향상과 습관 형성을 동시에!
하루 3문제로 실력 향상과 습관 형성을 동시에!
체리팟 교사용 기능으로
수업 전부터 방과후까지 스마트하게!
수업 전부터 방과후까지 스마트하게!
학급별 진도 설정 후 과제 생성하기
상황별 시나리오에 맞는 과제 운영
AI 기술로 실시간 풀이과정 분석
이해도가 낮은 학생은 바로바로 파악
과제 결과를 바탕으로 맞춤 학습까지!
이제 체리팟과 함께
효율적 수업 운영을 시작해보세요!
효율적 수업 운영을 시작해보세요!
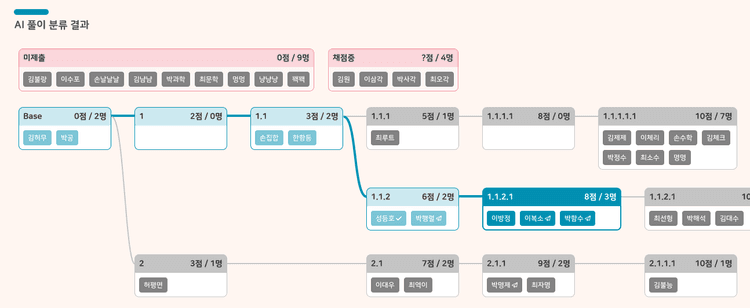
학습활동/과제 진행 중에 제출된 풀이는
AI가 실시간 채점 후 기준별로 분류해줍니다.
AI가 실시간 채점 후 기준별로 분류해줍니다.
체리팟의 교육적 효과성은
다양한 교육 현장에서 검증되었습니다
다양한 교육 현장에서 검증되었습니다
180개 이상의 학교에서
체리팟의 과정 중심 학습을 활용하였습니다.
체리팟의 과정 중심 학습을 활용하였습니다.
*온라인 교육 분야 비대면 스타트업 최우수 기업*
*교육부 에듀테크 컨텐츠 우수기업*
*교육부 에듀테크 컨텐츠 우수기업*
체리팟의 과정 중심 수학 학습,
지금 시작해보세요.
지금 시작해보세요.
디지털 선도학교 / AI 점핑 수학 학교 등
체리팟 이용을 희망하는 학교를 대상으로
무료 체험 프로그램을 운영 중입니다.
체리팟 이용을 희망하는 학교를 대상으로
무료 체험 프로그램을 운영 중입니다.
체리팟은 AI 기술 기반 에듀테크 기업
제제듀가 만들어나가고 있습니다.
제제듀가 만들어나가고 있습니다.
 미국/싱가포르 에듀테크 프로그램
미국/싱가포르 에듀테크 프로그램국내 스타트업 최초/유일 선정
정부와 글로벌 기업으로부터 검증된 회사입니다.